市场数据

定价与收益

用向量描述特定资产的时间序列。

有 NN 个资产，资产 ss 的时间序列为 Πs(t)\Pi_s(t)，其中 t=[T]t=[T]，s=[N]s=[N]；时间差标准化为 11，在应用中时间差可小到毫秒级别。

资产在时刻 tt 的收益定义在时间变化 Δt∈Z+\Delta t\in \mathbb Z_+ 上，资产 ss 的收益为 ys(t):=Πs(t)−Πs(t−Δt)Πs(t−Δt)y_s(t):=\frac{\Pi_s(t)-\Pi_s(t-\Delta t)}{\Pi_s(t-\Delta t)}。

期望收益与协方差矩阵

向量 y⃗(t)\vec{y}(t) 表示 NN 个资产时刻 tt 的收益。定义未来 Δt\Delta t 后的收益为 Y⃗\vec{Y}，其期望为

R⃗id:=E[Y⃗]\vec{R}^{\text{id}}:=\mathbb{E}\left[\vec{Y}\right]

根据历史收益，R⃗id\vec{R}^{\text{id}} 可估计为

R⃗=1T∑t=1Ty⃗(t)\vec{R}=\frac{1}{T}\sum_{t=1}^T \vec{y}(t)

定义收益协方差矩阵为

Σid=V[(Y⃗−R⃗id)(Y⃗−R⃗id)T]\Sigma^{\text{id}}=\mathbb{V}\left[\left(\vec{Y}-\vec{R}^{\text{id}}\right)\left(\vec{Y}-\vec{R}^{\text{id}}\right)^\mathrm{T}\right]

根据历史收益，Σid\Sigma^{\text{id}} 可估计为

Σ=1T−1∑t=1T(y⃗(t)−R⃗)(y⃗(t)−R⃗)T\Sigma=\frac{1}{T-1}\sum_{t=1}^T \left(\vec{y}(t)-\vec{R}\right)\left(\vec{y}(t)-\vec{R}\right)^\mathrm{T}

量子计算机中的市场数据

数据获取

数据访问用 qRAM 实现。令 did_i 表示 mm 比特的市场数据近似，存储在第 ii 个 qRAM 中，其中 i=[NqRAM]i=\left[N_{\text{qRAM}}\right]。有一个 log⁡2NqRAM\log_2 N_{\text{qRAM}} 比特量子寄存器，表示所访问的 qRAM 编号。

qRAM允许对数据的并行访问，一次查询操作可表示为：

∑i=1NqRAMαi∣i⟩∣0⟩⊗m→∑i=1NqRAMαi∣i⟩∣di⟩\sum_{i=1}^{N_{\text{qRAM}}}\alpha_i|i\rangle|0\rangle^{\otimes m}\to\sum_{i=1}^{N_{\text{qRAM}}}\alpha_i|i\rangle|d_i\rangle

输入

TT 个时间片，NN 个投资品的时间序列。

∣s⟩∣t⟩∣0⟩⊗m→∣s⟩∣t⟩∣Πs(t)⟩|s\rangle|t\rangle|0\rangle^{\otimes m}\to|s\rangle|t\rangle|\Pi_s(t)\rangle

可构造

∣s⟩∣t⟩∣0⟩⊗m→∣s⟩∣t⟩∣ys(t)⟩|s\rangle|t\rangle|0\rangle^{\otimes m}\to|s\rangle|t\rangle|y_s(t)\rangle

引入辅助比特，用受控旋转门得到与收益向量 y⃗(t)\vec{y}(t) 有关的量子态

∣ys(t)⟩∣0⟩→∣ys(t)⟩(1−δ2ys2(t)∣0⟩+δys(t)∣1⟩)|y_s(t)\rangle|0\rangle\to|y_s(t)\rangle\left(\sqrt{1-\delta^2y_s^2(t)}|0\rangle+\delta y_s(t)|1\rangle\right)

当辅助比特测量为 11 时（成功概率 δ2TN∑t=1T∑s=1Nys2(t)\frac{\delta^2}{TN}\sum_{t=1}^T\sum_{s=1}^N y_s^2(t)）

1∣y∣∑t=1T∑s=1Nys(t)∣t⟩∣s⟩=1∣y∣∑t=1T∣y⃗(t)∣∣t⟩∣y⃗(t)⟩=:∣χ⟩\frac{1}{|y|}\sum_{t=1}^T\sum_{s=1}^Ny_s(t)|t\rangle|s\rangle= \frac{1}{|y|}\sum_{t=1}^T|\vec{y}(t)||t\rangle|\vec{y}(t)\rangle=:|\chi\rangle

其中

∣y∣2=∑t=1T∑s=1Nys2(t)=∑t=1T∣y⃗(t)∣2|y|^2=\sum_{t=1}^T\sum_{s=1}^Ny_s^2(t)=\sum_{t=1}^T|\vec{y}(t)|^2

∣y⃗(t)⟩:=1∣y⃗(t)∣∑s=1Nys(t)∣s⟩|\vec{y}(t)\rangle:=\frac{1}{|\vec{y}(t)|}\sum_{s=1}^N y_s(t)|s\rangle

期望收益

对 ∣χ⟩|\chi\rangle 中的 ∣t⟩|t\rangle 做 Hadamard operation 然后测量 00 态

1T∑t=1T⟨t∣χ⟩→1∣y′∣∑s=1N(∑t=1Tys(t))∣s⟩≡∣R⃗⟩\frac{1}{\sqrt{T}}\sum_{t=1}^T\langle t|\chi\rangle\to\frac{1}{|y^\prime|}\sum_{s=1}^N\left(\sum_{t=1}^T y_s(t) \right)|s\rangle\equiv|\vec{R}\rangle

协方差矩阵

投资组合优化

投资组合优化问题可以表述为一个等式约束的二次规划问题：对于固定的标准差（风险偏好），找到最大化期望收益的投资组合；或者等价地，对于固定的期望收益，找到最小化收益标准差的投资组合。

投资品的风险用投资品收益的标准差衡量，标准差越大风险越大。

风险-收益空间

风险收益空间

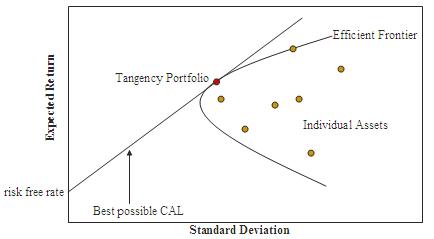
转化为线性方程

今日资产价值用向量 Π⃗\vec{\Pi} 表示，期望收益为 R⃗\vec{R}，协方差矩阵为 Σ\Sigma。投资者总资产为 ξ\xi，每个投资品买的数量为 w⃗\vec{w}。投资组合满足约束 ξ=Π⃗Tw⃗\xi=\vec{\Pi}^{\mathrm T}\vec{w}，期望收益 R⃗Tw⃗\vec{R}^\mathrm{T}\vec{w}。投资者希望获得预期收益 μ=R⃗Tw⃗\mu=\vec{R}^\mathrm{T}\vec{w}，并最小化风险 w⃗TΣw⃗\vec{w}^\mathrm{T}\Sigma\vec{w}。

min⁡w⃗w⃗TΣw⃗s.t.R⃗Tw⃗=μΠ⃗Tw⃗=ξ\begin{aligned} \min_{\vec{w}}&\quad \vec{w}^\mathrm{T}\Sigma\vec{w}\\ \text{s.t.}&\quad \vec{R}^\mathrm{T}\vec{w}=\mu\\ &\quad \vec{\Pi}^\mathrm{T}\vec{w}=\xi \end{aligned}

引入拉格朗日乘子得 Mx⃗=b⃗M\vec{x}=\vec{b}

[00R⃗T00Π⃗TR⃗Π⃗Σ][ηθw⃗]=[μξ0⃗]\begin{bmatrix} 0&0&\vec{R}^\mathrm{T}\\ 0&0&\vec{\Pi}^\mathrm{T}\\ \vec{R}&\vec{\Pi}&\Sigma \end{bmatrix} \begin{bmatrix} \eta\\ \theta\\ \vec{w} \end{bmatrix} = \begin{bmatrix} \mu\\ \xi\\ \vec{0} \end{bmatrix}

HHL

产生量子态的用途

  • 测量风险 τ=⟨w∣Σ∣w⟩\tau=\langle w|\Sigma|w\rangle。

  • 绘制风险-收益曲线。

  • 用别的方案 ∣w~⟩|\tilde{w}\rangle 和 ∣w⟩|w\rangle 进行swap test，验证 ∣w~⟩|\tilde{w}\rangle 的合理性。

  • 测量 ⟨Psector∣w⟩\langle P_{\text{sector}}|w\rangle，得到某一部分的权重。

  • 对 ∣w⟩|w\rangle 采样

    • 采样 MM 次，∣wj′⟩:=MjM|w_j^\prime\rangle:=\sqrt{\frac{M_j}{M}}。

    • long/short assumption：wj′=sign(Rj)MjMw_j^\prime=\text{sign}(R_j)\sqrt{\frac{M_j}{M}}

      • E[Rjwj′]\mathbb{E}\left[\frac{R_j}{w_j^\prime}\right] 为最优投资组合的期望收益。

      • ∣w′⟩|w^\prime\rangle 包含原始风险和采样误差的风险，采样误差风险为 O(1M)\mathcal{O}\left(\frac{1}{M}\right)。