简介

伸展树，英文名 Splay\text{Splay}，是一种有旋的平衡树，它通过不断将某个节点旋转到根节点，使得整棵树仍然满足二叉查找树的性质，并且保持平衡而不至于退化为链，它由 Daniel Sleator\text{Daniel Sleator} 和 Robert Tarjan\text{Robert Tarjan} 发明。
Splay\text{Splay} 维护的信息如下。

rootroot tottot fatherifather_i son(i,0/1)son(i,0/1) valival_i cnticnt_i SizeiSize_i
根节点 节点数量 父亲节点 左右儿子 节点权值 权值出现次数 子树大小

伸展树的操作

函数名

1
2
3
4
5
6
7
8
9
10
11
void del(int);//删除元素
int Pre();//前驱
int Next();//后继
void splay(int);//伸展
int Rank(int);//k的排名
void insert(int);//插入
int k_th(int);//第k名
void rotate(int);//旋转
void maintain(int);//更新节点信息
bool RightSon(int);//判断节点类型
void clear(int);//清空节点

三个基础操作

维护子树大小。

1
2
3
void maintain(int x){
	Size[x]=Size[son[x][0]]+Size[son[x][1]]+cnt[x];
}

判断节点类型，是右儿子则返回真，是左儿子返回假。

1
2
3
bool RightSon(int x){
	return x==son[father[x]][1];
}

初始化节点信息。

1
2
3
4
void clear(int x){
	memset(son[x],0,sizeof(son[x]));
	father[x]=Size[x]=val[x]=cnt[x]=0;
}

旋转操作

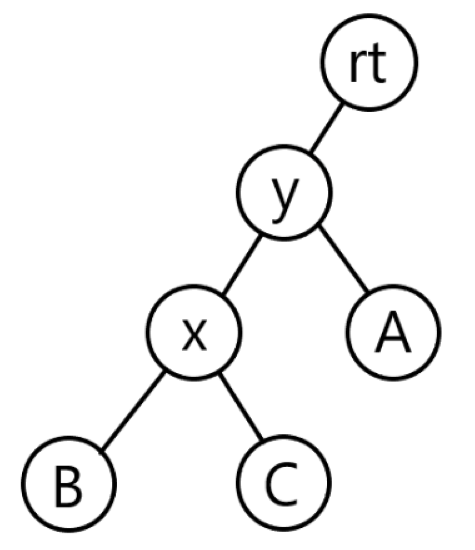
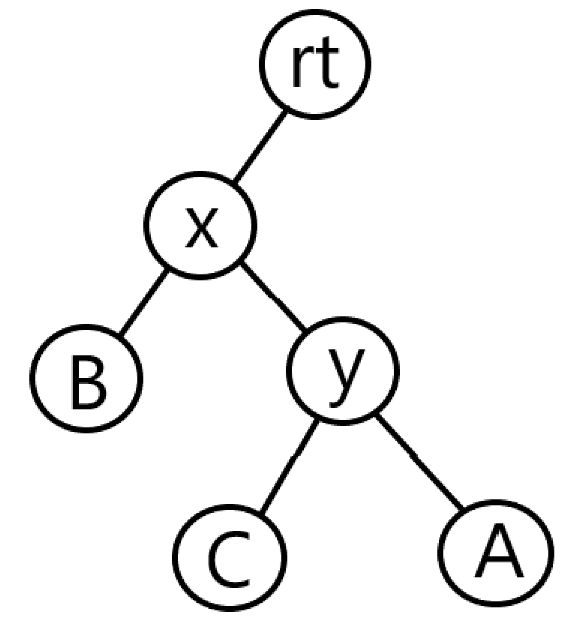
旋转是有旋平衡树的重要操作。Splay\text{Splay} 的旋转分为左旋（ZAG\text{ZAG}）和右旋（ZIG\text{ZIG}），一般对右儿子进行左旋，对左儿子进行右旋。
如图，为右旋 xx 的操作。右旋后，要将原来的 xx 的右儿子挂在 yy 的左儿子上。
1.png ⟹\Longrightarrow 2.png
如图，为左旋 yy 的操作。左旋后，要将原来 yy 的左儿子挂在 xx 的右儿子上。
2.png ⟹\Longrightarrow 1.png

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
void rotate(int x){
	//旋转一次
	int y=father[x];//父亲
	int rt=father[y];//祖父
	//右儿子为x则k为1
	//否则x为左儿子 k=0
	int k=RightSon(x);
	//ZIG 右挂左
	//ZAG 左挂右
	son[y][k]=son[x][k^1];
	father[son[x][k^1]]=y;
	son[x][k^1]=y;
	//更新
	father[y]=x;
	father[x]=rt;
	if(rt){
		son[rt][y==son[rt][1]]=x;
	}
	//更新节点信息
	maintain(x);
	maintain(y);
}

伸展操作

每访问一个节点后都要强制将其旋转到根节点，我们称这样的操作为伸展（splay\text{splay}）。这类似 cache\text{cache} 的 LRU\text{LRU} 算法，最近被访问的信息总能在较短时间内获得。伸展操作是由多次旋转操作组成的，最终会将需要伸展到根节点的节点 xx 到根节点。每次旋转操作具体分为 66 种情况讨论，其中定义 xx 为需要旋转到根的节点。
当 xx 的父亲为根节点时：若 xx 为左儿子，就进行一次 ZIG\text{ZIG}；若 xx 为右儿子，就进行一次 ZAG\text{ZAG}。
splay1.png splay2.png
当 xx 与其父亲节点 ff 同类时：若 xx 和 ff 都为左儿子，对 ff 进行一次 ZIG\text{ZIG}，再对 xx 进行一次 ZIG\text{ZIG}；若 xx 和 ff 都为右儿子，对 ff 进行一次 ZAG\text{ZAG}，再对 xx 进行一次 ZAG\text{ZAG}。
splay4.png splay3.png
当 xx 与其父亲节点 ff 不同类时：若 xx 为右儿子，ff 为左儿子，对 xx 进行一次 ZAG\text{ZAG}，再对 xx 进行一次 ZIG\text{ZIG}；若 xx 为 左儿子，ff 为右儿子，对 xx 进行一次 ZIG\text{ZIG}，再对 xx 进行一次 ZAG\text{ZAG}。
splay5.png splay6.png

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
void splay(int x){
	int f=father[x];
	//考察f和x 进行多组旋转将x伸展到根节点
	while(f){
		if(father[f]){
			if(RightSon(f)==RightSon(x)){
				//同类节点
				rotate(f);
			}else{
				rotate(x);
			}
		}
		rotate(x);//每组操作最后一步必定是旋转x
		f=father[x];
	}
	root=x;//更新根节点
}

插入操作

假设要插入数字 kk。
如果树空，则直接插入根并退出。
如果当前节点的权值等于 kk，那么只要增加当前节点的大小并更新节点和父亲的信息，最后当前节点进行 splay\text{splay} 操作。
否则按照二叉查找树的性质向下找，找到空节点就插入即可，最后将插入的节点进行 splay\text{splay} 操作。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
void insert(int k){
	//树空直接插入
	if(!root){
		val[++tot]=k;
		cnt[tot]++;
		root=tot;
		maintain(root);
		return;
	}
	int cur=root,f=0;
	while(1){
		if(val[cur]==k){
		//如果当前节点的权值等于k则增加当前节点的大小
		//并更新节点和父亲的信息 将当前节点splay
			cnt[cur]++;
			maintain(cur);
			maintain(f);
			splay(cur);
			break;
		}
		f=cur;
		cur=son[cur][val[cur]<k];//沿二叉BST前进
		if(!cur){
			//找到空节点插入即可
			//插入后splay
			val[++tot]=k;
			cnt[tot]++;
			father[tot]=f;
			son[f][val[f]<k]=tot;
			maintain(tot);
			maintain(f);
			splay(tot);
			break;
		}
	}
}

删除操作

设删除的某个数字为 kk。
首先对 kk 所在节点进行伸展操作，这一步可由int Rank(k) 实现。此时，若 cntroot>1cnt_{root}>1，那么直接将 cntrootcnt_{root} 减 11 并返回；否则，合并 rootroot 的左右子树，赋予新的根节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
void del(int k){
	//找到权值为k的点x
	//首先将x旋转到根的位置
	//前两步用Rank函数实现
	//若 cnt[x]>1，那么将cnt[x]减1并退出
	//否则，合并它的左右两棵子树
	int _=Rank(k);
	if(cnt[root]>1){
		cnt[root]--;
		maintain(root);
		return;
	}
	if(!son[root][0]&&!son[root][1]){
		//只有单个点
		clear(root);
		root=0;
		return;
	}
	if(!son[root][0]){
		//只有右子树
		int cur=root;
		root=son[root][1];
		father[root]=0;
		clear(cur);
		return;
	}
	if(!son[root][1]){
		//只有左子树
		int cur=root;
		root=son[cur][0];
		father[root]=0;
		clear(cur);
		return;
	}
	int cur=root;
	int x=Pre();//找到根节点的前驱 同时将x作为根节点
	//更新
	father[son[cur][1]]=x;//原来根的右子树的父亲为x
	son[x][1]=son[cur][1];//x的右子树
	clear(cur);
	maintain(root);
}

查询操作

所有的查询操作都基于 BST\text{BST} 的性质，而最后将查询的节点进行伸展操作体现了伸展树的独特性质。

查询数字 kk 的排名

设当前节点为 curcur。若 k<valcurk<val_{cur}，向 curcur 的左子树寻找；若 k>valcurk>val_{cur}，将答案加上左子树和当前节点的大小，继续向右子树寻找；若 k=valcurk=val_{cur}，将当前结果加 11 就是排名，直接返回排名。
注意最后需要进行伸展操作。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
int Rank(int k){
	//按照BST搜索排名
	int res=0;
	int cur=root;
	while(1){
		if(k<val[cur]){
			//若x比当前节点的权值小
			//向其左子树查找
			cur=son[cur][0];
		}else{
			//如果x比当前节点的权值大
			//将res排名加上cur的左子树大小和cur的cnt
			//如果x与当前点的权值相同，将答案加1并返回
			res+=Size[son[cur][0]];
			if(k==val[cur]){
				splay(cur);//最近用到的要splay
				return ++res;
			}
			res+=cnt[cur];
			cur=son[cur][1];
		}
	}
}

查询排名 kk 的数

设当前访问节点为 curcur，并将 kk 视作剩余排名。
如果 curcur 的左子树非空且剩余排名 kk 不大于左子树的大小，那么向左子树查找；否则将 kk 减去左子树和 curcur 的大小，如果此时 k⩾0k\geqslant 0，则直接返回 valcurval_{cur}，不然则继续向右子树查找。
注意最后要进行伸展操作。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
int k_th(int k){
	int cur=root;
	while(1){
		if(son[cur][0]&&k<=Size[son[cur][0]]){
			//左子树非空
			//剩余排名不大于左子树的size
			cur=son[cur][0];
		}else{
			//将k减去左子树的和根的大小
			//此时若k<=0, 返回cur的值
			//否则继续找右子树
			k-=cnt[cur]+Size[son[cur][0]];
			if(k<=0){
				splay(cur);
				return val[cur];
			}
			cur=son[cur][1];
		}
	}
}

查询 xx 的前驱

前驱定义为小于 xx 的最大的数。
根据伸展树的性质，我们不妨先插入 xx，此时就有 valroot=xval_{root}=x。此时，前驱即为 rootroot 的左子树中最右边的节点。
找到前驱后直接将 xx 删除即可。

1
2
3
4
5
6
7
8
9
10
insert(x);
int Pre(){
	int cur=son[root][0];
	while(son[cur][1]){
		cur=son[cur][1];
	}
	splay(cur);
	return cur;
}
del(x);

查询 xx 的后继

后继定义为大于 xx 的最小的数。
根据伸展树的性质，我们不妨先插入 xx，那么就有 valroot=xval_{root}=x。此时，后继即为 rootroot 的右子树中最左边的节点。
找到后继后直接删除 xx 即可。

1
2
3
4
5
6
7
8
9
10
insert(x);
int Next(){
	int cur=son[root][1];
	while(son[cur][0]){
		cur=son[cur][0];
	}
	splay(cur);
	return cur;
}
del(x);

P3369 【模板】普通平衡树 ↬\looparrowright

题目描述

您需要写一种数据结构（可参考题目标题），来维护一些数，其中需要提供以下操作：
插入 xx 数；
删除 xx 数（若有多个相同的数，因只删除一个）；
查询 xx 数的排名（排名定义为比当前数小的数的个数加 11）；
查询排名为 xx 的数；
求 xx 的前驱（前驱定义为小于 xx，且最大的数）；
求 xx 的后继（后继定义为大于 xx，且最小的数）。

输入格式

第一行为 nn，表示操作的个数,下面 nn 行每行有两个数 optopt 和 xx，optopt 表示操作的序号 （1⩽opt⩽61 \leqslant opt \leqslant 6）。

输出格式

对于操作 3,4,5,63,4,5,6 每行输出一个数，表示对应答案

输入输出样例

输入 #1

1
2
3
4
5
6
7
8
9
10
11
10
1 106465
4 1
1 317721
1 460929
1 644985
1 84185
1 89851
6 81968
1 492737
5 493598

输出 #1

1
2
3
106465
84185
492737

说明/提示

对于 100%100\% 的数据，1⩽n⩽1051\leqslant n \leqslant 10^5，∣x∣⩽107|x| \leqslant 10^7。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int N=100006;
int father[N];//父亲节点
int son[N][2];//儿子节点
int Size[N];//子树大小
int val[N];//节点权值
int tot;//节点数
int root;//根节点
int cnt[N];//节点大小
void del(int);//删除元素
int Pre();//前驱
int Next();//后继
void splay(int);//伸展
int Rank(int);//k的排名
void insert(int);//插入
int k_th(int);//第k名
void rotate(int);//旋转
void maintain(int);//更新节点信息
bool RightSon(int);//判断节点类型
void clear(int);//清空节点
int main(){
	int n;
	cin>>n;
	while(n--){
		short opt;
		int x;
		scanf("%hd%d",&opt,&x);
		switch(opt)
		{
		case 1: 
			insert(x);
			break;
		case 2:
			del(x);
			break;
		case 3:
			printf("%d\n",Rank(x));
			break;
		case 4:
			printf("%d\n",k_th(x));
			break;
		case 5:
			insert(x);
			printf("%d\n",val[Pre()]);
			del(x);
			break;
		case 6:
			insert(x);
			printf("%d\n",val[Next()]);
			del(x);
			break;
		}
	}
	return 0;
}
void maintain(int x){
	Size[x]=Size[son[x][0]]+Size[son[x][1]]+cnt[x];
}
bool RightSon(int x){
	return x==son[father[x]][1];
}
void clear(int x){
	memset(son[x],0,sizeof(son[x]));
	father[x]=Size[x]=val[x]=cnt[x]=0;
}
void rotate(int x){
	//旋转一次
	int y=father[x];//父亲
	int rt=father[y];//祖父
	//右儿子为x则k为1
	//否则x为左儿子 k=0
	int k=RightSon(x);
	//ZIG 右挂左
	//ZAG 左挂右
	son[y][k]=son[x][k^1];
	father[son[x][k^1]]=y;
	son[x][k^1]=y;
	//更新
	father[y]=x;
	father[x]=rt;
	if(rt){
		son[rt][y==son[rt][1]]=x;
	}
	maintain(x);
	maintain(y);
}
void del(int k){
	//找到权值为k的点x
	//首先将x旋转到根的位置
	//前两步用Rank函数实现
	//若 cnt[x]>1，那么将cnt[x]减1并退出
	//否则，合并它的左右两棵子树
	int _=Rank(k);
	if(cnt[root]>1){
		cnt[root]--;
		maintain(root);
		return;
	}
	if(!son[root][0]&&!son[root][1]){
		//只有单个点
		clear(root);
		root=0;
		return;
	}
	if(!son[root][0]){
		//只有右子树
		int cur=root;
		root=son[root][1];
		father[root]=0;
		clear(cur);
		return;
	}
	if(!son[root][1]){
		//只有左子树
		int cur=root;
		root=son[cur][0];
		father[root]=0;
		clear(cur);
		return;
	}
	int cur=root;
	int x=Pre();//找到根节点的前驱 同时将x作为根节点
	//更新
	father[son[cur][1]]=x;//原来根的右子树的父亲为x
	son[x][1]=son[cur][1];//x的右子树
	clear(cur);
	maintain(root);
}
int Pre(){
	int cur=son[root][0];
	while(son[cur][1]){
		cur=son[cur][1];
	}
	splay(cur);
	return cur;
}
int Next(){
	int cur=son[root][1];
	while(son[cur][0]){
		cur=son[cur][0];
	}
	splay(cur);
	return cur;
}
void splay(int x){
	int f=father[x];
	while(f){
		if(father[f]){
			if(RightSon(f)==RightSon(x)){
				rotate(f);
			}else{
				rotate(x);
			}
		}
		rotate(x);//每组操作最后一步必定是旋转x
		f=father[x];
	}
	root=x;//更新根节点
}
void insert(int k){
	//树空直接插入
	if(!root){
		val[++tot]=k;
		cnt[tot]++;
		root=tot;
		maintain(root);
		return;
	}
	int cur=root,f=0;
	while(1){
		if(val[cur]==k){
		//如果当前节点的权值等于k则增加当前节点的大小
		//并更新节点和父亲的信息 将当前节点splay
			cnt[cur]++;
			maintain(cur);
			maintain(f);
			splay(cur);
			break;
		}
		f=cur;
		cur=son[cur][val[cur]<k];//沿二叉搜索前进
		if(!cur){
			//找到空节点插入即可
			//插入后splay
			val[++tot]=k;
			cnt[tot]++;
			father[tot]=f;
			son[f][val[f]<k]=tot;
			maintain(tot);
			maintain(f);
			splay(tot);
			break;
		}
	}
}
int Rank(int k){
	//按照BST搜索排名
	int res=0;
	int cur=root;
	while(1){
		if(k<val[cur]){
			//若x比当前节点的权值小
			//向其左子树查找
			cur=son[cur][0];
		}else{
			//如果x比当前节点的权值大
			//将res排名加上cur的左子树大小和cur的cnt
			//如果x与当前点的权值相同，将答案加1并返回
			res+=Size[son[cur][0]];
			if(k==val[cur]){
				splay(cur);//最近用到的要splay
				return ++res;
			}
			res+=cnt[cur];
			cur=son[cur][1];
		}
	}
}
int k_th(int k){
	int cur=root;
	while(1){
		if(son[cur][0]&&k<=Size[son[cur][0]]){
			//左子树非空
			//剩余排名不大于左子树的size
			cur=son[cur][0];
		}else{
			//将k减去左子树的和根的大小
			//此时若k<=0, 返回cur的值
			//否则继续找右子树
			k-=cnt[cur]+Size[son[cur][0]];
			if(k<=0){
				splay(cur);
				return val[cur];
			}
			cur=son[cur][1];
		}
	}
}

P3391 【模板】文艺平衡树 ↬\looparrowright

题目描述

您需要写一种数据结构，来维护一个有序数列。
其中需要提供以下操作：翻转一个区间，例如原有序序列是 5 4 3 2 15\ 4\ 3\ 2\ 1，翻转区间是 [2,4][2,4] 的话，结果是 5 2 3 4 15\ 2\ 3\ 4\ 1。

输入格式

第一行两个正整数 n,mn,m，表示序列长度与操作个数。序列中第 ii 项初始为 ii。
接下来 mm 行，每行两个正整数 l,rl,r，表示翻转的区间。

输出格式

输出一行 nn 个正整数，表示原始序列经过 mm 次变换后的结果。

输入输出样例

输入 #1

1
2
3
4
5 3
1 3
1 3
1 4

输出 #1

1
4 3 2 1 5

说明/提示

对于 100%100\% 的数据，1⩽n,m⩽1000001 \leqslant n, m \leqslant 100000，1⩽l⩽r⩽n1 \leqslant l \leqslant r \leqslant n。

分析

首先按照中序遍历建树，然后对于每次修改区间 l,rl,r，首先得获取这段区间在搜索树中的位置。
方法是利用伸展树，将 ll 的前趋 l−1l-1 旋转到根节点，将 rr 的后继 r+1r+1 旋转到根节点的右儿子。经过这个操作后，根节点的右儿子的左子树的就是区间 [l,r][l,r]。
翻转时，因为树是中序遍历，所以我们只要将 [l,r][l,r] 这个区间子树左右儿子的节点交换位置，这样再中序遍历相当于先访问右儿子再访问根节点，最后访问左儿子，即做到了翻转操作。
为了降低复杂度，需要对翻转进行优化，我们用到懒惰标记 lazyxlazy_x（表示x是否翻转），每次翻转时只要某个节点有标记且在翻转的区间内，则将标记下放给它的两个儿子节点且将自身标记清 00，这样便避免了多余的重复翻转。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
const int N=100006;
int n,m;
int tot;
int Size[N];
int father[N];
bool lazy[N];
int val[N];
int son[N][2];
int ans[N];
int root;
inline void pushup(int);
inline void pushdown(int);
inline bool RightSon(int);
void rotate(int);
int find(int);
void splay(int,int);
int build(int,int,int);
void DFS(int);
int main(){
	cin>>n>>m;
	int i;
	for(i=1;i<=n+2;i++){
		ans[i]=i-1;
	}
	root=build(1,n+2,0);
	for(i=1;i<=m;i++){
		int l,r;
		scanf("%d%d",&l,&r);
		l=find(l);//l-1 的排名为l
		r=find(r+2);//r+1的排名为r+2
		splay(l,0);
		splay(r,l);
		lazy[son[son[root][1]][0]]^=1;
	}
	DFS(root);
	for(i=2;i<=n+1;i++){
		printf("%d",ans[i]);
		putchar(i==n+1?'\n':' ');
	}
	return 0;
}
int build(int l,int r,int rt){
	int cur=l+r>>1;
	father[cur]=rt;
	val[cur]=ans[cur];
	if(l<cur){
		son[cur][0]=build(l,cur-1,cur);
	}
	if(r>cur){
		son[cur][1]=build(cur+1,r,cur);
	}
	pushup(cur);
	return cur;
}
void DFS(int cur){
	pushdown(cur);
	if(son[cur][0]){
		DFS(son[cur][0]);
	}
	ans[++tot]=val[cur];
	if(son[cur][1]){
		DFS(son[cur][1]);
	}
}
inline void pushup(int rt){
	Size[rt]=Size[son[rt][0]]+Size[son[rt][1]]+1;
}
inline void pushdown(int rt){
	if(lazy[rt]){
		lazy[son[rt][0]]^=1;
		lazy[son[rt][1]]^=1;
		swap(son[rt][0],son[rt][1]);
		lazy[rt]=0;
	}
}
inline bool RightSon(int x){
	return x==son[father[x]][1];
}
void rotate(int x){
	int y=father[x];
	int rt=father[y];
	//右儿子为x则k为1
	//否则x为左儿子 k=0
	int k=RightSon(x);
	//ZIG 右挂左
	//ZAG 左挂右
	son[y][k]=son[x][k^1];
	father[son[x][k^1]]=y;
	son[x][k^1]=y;
	//更新
	father[y]=x;
	father[x]=rt;
	if(rt){
		son[rt][y==son[rt][1]]=x;
	}
	pushup(x);
	pushup(y);
}
void splay(int x,int p){
	while(father[x]!=p){
		int y=father[x];
		int rt=father[y];
		if(rt==p){
			rotate(x);
		}else{
			if(RightSon(x)==RightSon(y)){
				rotate(y);
			}else{
				rotate(x);
			}
			rotate(x);
		}
	}
	if(!p){
		root=x;
	}
}
int find(int x){
	int cur=root;
	while(1){
		pushdown(cur);
		if(son[cur][0]&&x<=Size[son[cur][0]]){
			//若存在左子树且x小于等于左子树的节点数，则x在左子树上
			cur=son[cur][0];
		}else{
			int left=1;
			if(son[cur][0]){
				left+=Size[son[cur][0]];
			}
			if(x==left){
				return cur;//排名消耗殆尽
			}else{
				x-=left;
				cur=son[cur][1];
			}
		}
	}
}