传送门 ↬\looparrowright

Problem Description

On the beaming day of 60th anniversary of NJUST, as a military college which was Second Artillery Academy of Harbin Military Engineering Institute before, queue phalanx is a special landscape.
Here is a m×nm\times n rectangle, and this one can be divided into m×nm\times n squares which are of the same size. As shown in the figure below.
01–02–03–04
||||&|| &||
05–06–07–08
||||&|| &||
09–10–11–12
Consequently, we have (m+1)×(n+1)(m+1)\times (n+1) nodes, which are all connected to their adjacent nodes. And actual queue phalanx will go along the edges.
The ID of the first node,the one in top-left corner, is 11. And the ID increases line by line first, and then by column in turn, as shown in the figure above.
For every node, there are two viable paths:
(1) go downward, indicated by D;
(2) go right, indicated by R.
The current mission is that, each queue phalanx has to walk from the left-top node No.1 to the right-bottom node whose ID is (m+1)×(n+1)(m+1)\times (n+1).
In order to make a more aesthetic marching, each queue phalanx has to conduct two necessary actions. Let’s define the action:
An action is started from a node to go for a specified travel mode.
So, two actions must show up in the way from 11 to (m+1)×(n+1)(m+1)\times (n+1).
For example, as to a 3×23\times 2 rectangle, figure below.
01–02–03–04
||||&|| &||
05–06–07–08
||||&|| &||
09–10–11–12
Assume that the two actions are (1)RRD (2)DDR
As a result , there is only one way : RRDDR. Briefly, you can not find another sequence containing these two strings at the same time.
If given the n,mn,m and two actions, can you calculate the total ways of walking from node No.1 to the right-bottom node?

Input

The first line contains a number TT, ( TT is about 100100, including 9090 small test cases and 1010 large ones) denoting the number of the test cases.
For each test cases,the first line contains two positive integers mm and nn (For large test cases,1≤m,n≤1001\le m,n\le 100, and for small ones 1≤m,n≤401\le m,n\le40) . mm denotes the row number and nn denotes the column number.
The next two lines each contains a string which contains only R and D. The length of string will not exceed 100100. We ensure there are no empty strings and the two strings are different.

Output

For each test cases,print the answer mod 10000000071000000007 in one line.

Sample Input

2
3 2
RRD
DDR
3 2
R
D

Sample Output

1
10

Idea

两种 action\text{action}，可以视为两个模式串，利用两个模式串可以建立 AC 自动机。
从坐标 (1,1)(1,1) 走向 (i,j)(i,j)，行走路线组成的字符串有多种，而对于两个模式串的存在情形，只存在四种状态，不妨进行状态压缩。00 代表两个模式串都不包含，01 代表仅包含第一个模式串，10 代表仅包含第二个模式串，11 代表两个模式串都包含。
插入字符串时，在字符串结尾标记改节点的状态，第一个模式串结尾标记为 01，第二个模式串结尾标记为 10。建立 AC 自动机时，利用 fail\mathrm{fail} 指针的性质，$\mathrm{fail}_x$ 指向节点 xx 所指代字符串的一个后缀，节点 xx 的状态应当与节点 $\mathrm{fail}_x$ 的状态叠加。如下图所示，DRD 为第一个模式串，RD 为第二个模式串；插入模式串时，节点 33 的状态为 01，节点 55 的状态为 10；叠加后，节点 33 的状态为 11，节点 55 的状态仍为 10。
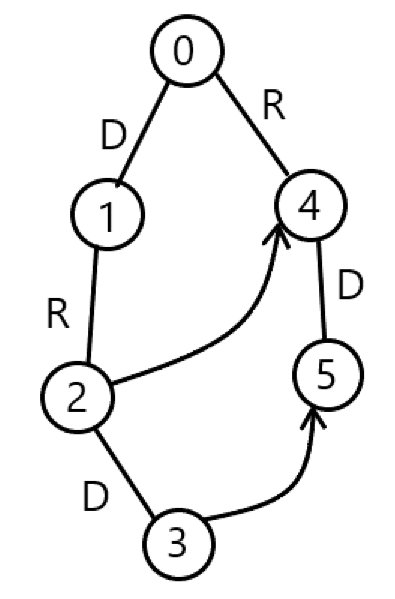
QQ截图20200720163851.png
采用状态压缩DP的方式，dp(i,j,k,l)dp(i,j,k,l) 表示实际走至坐标 (i,j)(i,j)，位于 AC 自动机的节点 kk，行走路线组成字符串状态为 ll 时的总方案数。由于只会出现 D 和 R 两个字符，将 D 映射为 00，R 映射为 11；那么就存在状态转移函数 trans(k,0)trans(k,0) 和 trans(k,1)trans(k,1)。考虑状态转移，若要向下走，则坐标转移至 (i+1,j)(i+1,j)，此时位于 AC 自动机的节点 trans(k,0)trans(k,0)，将状态 ll 与节点 trans(k,0)trans(k,0) 的状态叠加即为向下走一步后，行走路线组成的字符串的状态；向右走同理。走到 (m+1,n+1)(m+1,n+1) 时，可以停留在AC自动机的任意节点，最后得到的 ∑i=0totdp(m+1,n+1,i,3)\sum\limits_{i=0}^{tot}dp(m+1,n+1,i,3) 即为答案。

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
#include<cstring>
#include<iostream>
#include<algorithm>
#include<queue>
#include<cstdio>
using namespace std;
const int character_set=2;
const int MAX_STATE=4;
const int MAX_SIZE=110;
const int MAX_L=110;
const int mod=1000000007;
int _;
int m,n;
int tot;
int trie[MAX_L<<1][character_set];
int fail[MAX_L<<1];
short state[MAX_L<<1];
int dp[MAX_SIZE][MAX_SIZE][MAX_L<<1][MAX_STATE];
char str[MAX_L];
inline void init()
{
	memset(dp,0,sizeof(dp));
	memset(trie,0,sizeof(trie));
	memset(state,0,sizeof(state));
	memset(fail,0,sizeof(fail));
	tot=0;
}
/*
状态压缩
	00 两个字符串都不包含
	01 仅包含第一个字符串
	10 仅包含第二个字符串
	11 两个字符串都包含
*/
void insert(char s[],int pos)
{
	int len=strlen(s);
	int p=0,i;
	for(i=0;i<len;i++)
	{
		short ch;
		if(s[i]=='D') ch=0;
		else ch=1;
		if(!trie[p][ch]) trie[p][ch]=++tot;
		p=trie[p][ch];
	}
	state[p]|=(1<<pos);
}
void build_ACauto()
{
	int i;
	queue<int>q;
	for(i=0;i<character_set;i++)
	{
		if(trie[0][i])
		{
			q.push(trie[0][i]);
		}
	}
	while(!q.empty())
	{
		int x=q.front();
		q.pop();
		state[x]|=state[fail[x]];//状态叠加
		for(i=0;i<character_set;i++)
		{
			if(trie[x][i])
			{
				fail[trie[x][i]]=trie[fail[x]][i];
				q.push(trie[x][i]);
			}
			else trie[x][i]=trie[fail[x]][i];
		}
	}
}
int DP()
{
	int i,j,k,l;
	dp[1][1][0][0]=1;
	for(i=1;i<=m+1;i++)
	{
		for(j=1;j<=n+1;j++)
		{
			for(k=0;k<=tot;k++)
			{
				for(l=0;l<4;l++)
				{
					if(!dp[i][j][k][l]) continue;
					int p1=trie[k][0];//D
					int p2=trie[k][1];//R
					//状态叠加
					dp[i+1][j][p1][l|state[p1]]+=dp[i][j][k][l];//D
					dp[i][j+1][p2][l|state[p2]]+=dp[i][j][k][l];//R
					//取模
					dp[i+1][j][p1][l|state[p1]]%=mod;
					dp[i][j+1][p2][l|state[p2]]%=mod;
				}
			}
		}
	}
	int ans=0;
	for(i=0;i<=tot;i++) ans=(ans+dp[m+1][n+1][i][3])%mod;
	return ans%mod;
}
int main()
{
	for(cin>>_;_;_--)
	{
		init();
		scanf("%d%d",&m,&n);
		swap(m,n);
		scanf("%s",str);
		insert(str,0);
		scanf("%s",str);
		insert(str,1);
		build_ACauto();
		printf("%d\n",DP());
	}
	return 0;
}

Postscript

测试数据中，m,nm,n 的位置反了，这一点在原题的 discuss\text{discuss} 板块提到。
1.png