贝尔曼-福特算法(Bellman–Ford algorithm)

贝尔曼-福特算法是求解单源最短路径问题的一种算法，由 $\text{Richard Bellman}$ 和 $\text{Lester Ford}$ 创立的。有时候这种算法也被称为 $\text{Moore-Bellman-Ford}$ 算法，因为 $\text{Edward F. Moore}$ 也为这个算法的发展做出了贡献。它的原理是对图进行 $|V|-1$ 次松弛操作，得到所有可能的最短路径。其优于迪科斯彻算法的方面是边的权值可以为负数、实现简单，缺点是时间复杂度过高，高达 $O(|V||E|)$ 。但算法可以进行若干种优化，提高了效率。

迪杰斯特拉算法(Dijkstra’s algorithm)

算法思想

$\text{Dijkstra}$ 算法是由荷兰计算机科学家 $\text{Dijkstra}$ 在1956年发明的算法，并于3年后在期刊上发表。该算法使用类似广度优先搜索的方法解决赋权图的单源最短路径问题。
该算法存在很多变体：原始版本仅适用于找到两个顶点之间的最短路径，后来更常见的变体固定了一个顶点作为源结点然后找到该顶点到图中所有其它结点的最短路径，产生一个最短路径树。
该算法解决了图 $G=<V,E>$ 上带权的单源最短路径问题。具体来说， $\text{Dijkstra}$ 算法设置了一顶点集合 $S$ ，在集合 $S$ 中所有的顶点与源点 $s$ 之间的最终最短路径权值均已确定。算法反复选择最短路径估计最小的点 $u\in {V-S}$ 并将 $u$ 加入 $S$ 中。该算法常用于路由算法或者作为其他图算法的一个子模块。
应当注意，绝大多数的 $\text{Dijkstra}$ 算法不能有效处理带有负权边的图。
（来源：WikiPedia）

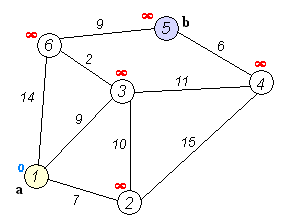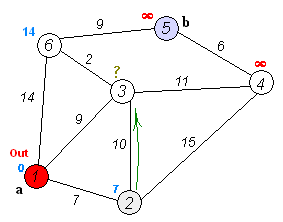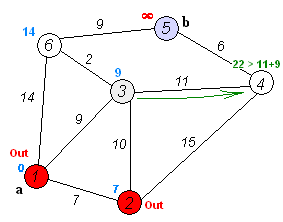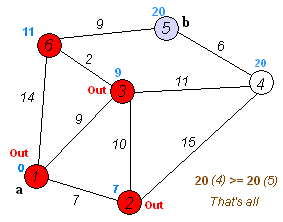
过程模拟

设 $dis[i]$ 为点 $v_0$ 到 $v_i$ 的最短路径长度，我们要一次求出 $dis[1],dis[2] ,\cdots ,dis[8]$ 。

我们每次选择最小的 $dis[i]$ 并标记为访问，初始时 $dis[0]=0,vis[0]=1$ 。
显然 $dis[1]=1$ ，我们标记 $v_1$ 已访问。由于 $v_1$ 还与 $v_2,v_3,v_4$ 相连，我们可以暂时设置 $dis[2]=dis[1]+w[1][2]=4$ , $dis[3]=dis[1]+w[1][3]=8$ , $dis[4]=dis[1]+w[1][4]=6$ 。

现在我们要求 $dis[2]$ ，如果说 $dis[2]=5$ ，那么就错了，刚才的另一条路径已经得到 $dis[2]=4<5$ ,我们标记 $v_2$ 已访问。由于 $v_2$ 还与 $v_4,v_5$ 连线，所以我们同时可以暂时设置 $dis[4]=5,dis[5]=11$ 。可以发现，这时 $dis[4]$ 已经被更新过了，得到了一个更小的值。

当我们要求 $dis[3]$ ，此时 $v_1,v_2$ 都已经被访问，我们从 $v_4$ 出发更新 $dis[3]$ ，得到 $dis[3]=7$ ， $vis[4]=1$ 。

$\cdots\cdots$ 可以按照上述过程一直推到 $dis[8]$ 。
可以看到，我们每次选择距离 $v_0$ 最近（ $dis[i]$ 最小）且还未被标记访问的点，从该点出发更新所有的 $dis[i]$ ，称之为松弛操作。

例题

POJ 2387 Til the Cows Come Home $\looparrowright$

Description

Bessie is out in the field and wants to get back to the barn to get as much sleep as possible before Farmer John wakes her for the morning milking. Bessie needs her beauty sleep, so she wants to get back as quickly as possible.
Farmer John’s field has $N$ $(2\leqslant N\leqslant 1000)$ landmarks in it, uniquely numbered $1..N$ . Landmark $1$ is the barn; the apple tree grove in which Bessie stands all day is landmark $N$ . Cows travel in the field using $T$ $(1\leqslant T\leqslant 2000)$ bidirectional cow-trails of various lengths between the landmarks. Bessie is not confident of her navigation ability, so she always stays on a trail from its start to its end once she starts it.
Given the trails between the landmarks, determine the minimum distance Bessie must walk to get back to the barn. It is guaranteed that some such route exists.

Input

Line 1: Two integers: $T$ and $N$
Lines 2…T+1: Each line describes a trail as three space-separated integers. The first two integers are the landmarks between which the trail travels. The third integer is the length of the trail, range 1…100.

Output

Line 1: A single integer, the minimum distance that Bessie must travel to get from landmark $N$ to landmark $1$ .

Sample Input

5 5
1 2 20
2 3 30
3 4 20
4 5 20
1 5 100

Sample Output

90

Hint

INPUT DETAILS

There are five landmarks.

OUTPUT DETAILS

Bessie can get home by following trails 4, 3, 2, and 1.

Translation

一张图有 $t$ 条边， $n$ 个点，求从节点 $1$ 至节点 $n$ 的最短路径长度。

Code

#include<iostream>
#include<cstring>
#include<algorithm>
#define N 1002
#define inf 0x3f3f3f3f
using namespace std;
int G[N][N];
int t,n;
bool vis[N];
int dis[N];
void dijkstra()
{
	int i,j;
	//赋初值
	for(i=1;i<=n;i++) dis[i]=G[1][i];
	int res,pos;
	vis[1]=1;//标记访问
	for(i=1;i<=n;i++)
	{
		res=inf;//初始化
		//找最小的dis[j]
		for(j=1;j<=n;j++)
		{
			if(res>dis[j]&&!vis[j])
			{
				pos=j;
				res=dis[j];
			}
		}
		vis[pos]=1;
		for(j=1;j<=n;j++)//松弛操作  
		{
			if(!vis[j]&&dis[j]>dis[pos]+G[pos][j])
			{
				dis[j]=dis[pos]+G[pos][j];
			}
		}
	}
	cout<<dis[n]<<endl;
}
void solve()
{
	//初始化
	memset(G,inf,sizeof(G));
	cin>>t>>n;
	int i;
	//构造邻接矩阵
	for(i=1;i<=n;i++) G[i][i]=0;
	while(t--)
	{
		int u,v,w;
		cin>>u>>v>>w;
		//避免重边，取最小值
		G[u][v]=min(G[u][v],w);
		G[v][u]=min(G[v][u],w);
	}
	dijkstra();
}
int main()
{
	solve();
	return 0;
}

优化

链式前向星优化

能极大降低空间复杂度，由于链式前向星可以存两点之间的很多边，所以不需要考虑去重边。

#include<iostream>
#include<cstring>
#include<algorithm>
#define N 5300
using namespace std;
int head[N];
int tot;
struct E
{
	int to;
	int Next;
	int w;
}edge[N];
//加边
void add_edge(int from,int to,int w)
{
	tot++;
	edge[tot].to=to;
	edge[tot].w=w;
	edge[tot].Next=head[from];
	head[from]=tot;
}
int t,n;
bool vis[N];
int dis[N];
void dijkstra()
{
	int i,j;
	memset(dis,0x3f,sizeof(dis));
	memset(vis,0,sizeof(vis));
	int res,pos;
	dis[1]=0;
	for(i=1;i<=n;i++)
	{
		res=0x3f3f3f3f;
		for(j=1;j<=n;j++)
		{
			if(res>dis[j]&&!vis[j])
			{
				pos=j;
				res=dis[j];
			}
		}
		vis[pos]=1;
		//遍历与pos相连的所有点
		for(j=head[pos];j!=-1;j=edge[j].Next)
		{
			int y=edge[j].to;
			if(!vis[y]&&dis[y]>dis[pos]+edge[j].w)
			{
				dis[y]=dis[pos]+edge[j].w;
			}
		}
	}
	cout<<dis[n]<<endl;
}
void solve()
{
	memset(head,-1,sizeof(head));
	cin>>t>>n;
	while(t--)
	{
		int u,v,w;
		cin>>u>>v>>w;
		add_edge(u,v,w);
		add_edge(v,u,w);
	}
	dijkstra();
}
int main()
{
	solve();
	return 0;
}

堆优化

堆优化可将时间复杂度降至 $O((m+n)\log n)$ 。使用一个优先队列来代替最短距离的查找。

#include<iostream>
#include<cstring>
#include<vector>
#include<queue>
#define N 5044
using namespace std;
int head[N];
int tot;
struct cmp//定义优先队列排序 
{
	template<typename T>
	bool operator()(T const& left,T const& right)
	{
		//second较大的在后 
		if(left.second>right.second) return true;
		else return false;
	}
};
struct E
{
	int to;
	int Next;
	int w;
}edge[N];
void add_edge(int from,int to,int w)
{
	tot++;
	edge[tot].to=to;
	edge[tot].w=w;
	edge[tot].Next=head[from];
	head[from]=tot;
}
int t,n;
bool vis[N];
int dis[N];
void dijkstra()
{
	int i,j;
	memset(dis,0x3f,sizeof(dis));
	memset(vis,0,sizeof(vis));
	int res,pos;
	dis[1]=0;
	priority_queue<pair<int,int>,vector<pair<int,int> >,cmp>q;
	q.push(make_pair(1,0));//代表顶点1，距离0。
	while(!q.empty())
	{
		pair<int,int>res;
		//弹出dis[i]最小的点 
		res=q.top();
		//该点被访问，删去 
		q.pop();
		int from=res.first;
		vis[from]=1;//标记 
		//松弛操作 
		for(j=head[from];j!=-1;j=edge[j].Next)
		{
			int to=edge[j].to;
			if(!vis[to]&&dis[to]>dis[from]+edge[j].w)
			{
				dis[to]=dis[from]+edge[j].w;
				//更新，压入优先队列 
				q.push(make_pair(to,dis[to])); 
			}
		}
	}
	cout<<dis[n];
}
void solve()
{
	memset(head,-1,sizeof(head));
	cin>>t>>n;
	while(t--)
	{
		int u,v,w;
		cin>>u>>v>>w;
		add_edge(u,v,w);
		add_edge(v,u,w);
	}
	dijkstra();
}
int main()
{
	solve();
	return 0;
}

模板

洛谷 P4779 【模板】单源最短路径（标准版） $\looparrowright$

题目描述

给定一个 $n$ 个点， $m$ 条有向边的带非负权图，请你计算从 $s$ 出发，到每个点的距离。
数据保证你能从 $s$ 出发到任意点。

输入格式

第一行为三个正整数 $n, m, s$ 。第二行起 $m$ 行，每行三个非负整数 $u_i, v_i, w_i$ ，表示从 $u_i$ 到 $v_i$ 有一条权值为 $w_i$ 的有向边。

输出格式

输出一行 $n$ 个空格分隔的非负整数，表示 $s$ 到每个点的最短距离。

输入输出样例

输入 #1

4 6 1
1 2 2
2 3 2
2 4 1
1 3 5
3 4 3
1 4 4

输出 #1

0 2 4 3

说明/提示

$1 \leq n \leq 10^5$ ；
$1 \leq m \leq 2\times 10^5$ ；
$1 \leq u_i, v_i\leq n$ ；
$0 \leq \sum w_i \leq 10 ^ 9$ 。

代码

#include<cstdio>
#include<algorithm>
#include<queue>
#define N 100002
using namespace std;
struct E
{
	int to;
	int w;
	int Next;
}edge[N<<1];
int head[N],tot;
int dis[N];
bool vis[N];
int n,m,s;
inline void add(int u,int v,int w)
{
	tot++;
	edge[tot].to=v;
	edge[tot].w=w;
	edge[tot].Next=head[u];
	head[u]=tot;
}
struct node
{
	int id;
	int dis;
	bool operator<(const node &x)const
	{
		return x.dis<dis;
	}
};
void dijkstra()
{
	fill(dis,dis+1+n,0x7fffffff);
	dis[s]=0;
	int i;
	priority_queue<node>q;
	q.push((node){s,0});
	while(!q.empty())
	{
		node now=q.top();
		q.pop();
		int x=now.id;
		if(vis[x]) continue;
		vis[x]=1;
		for(i=head[x];~i;i=edge[i].Next)
		{
			int y=edge[i].to;
			if(!vis[y]&&dis[y]>dis[x]+edge[i].w)
			{
				dis[y]=dis[x]+edge[i].w;
				q.push((node){y,dis[y]});
			}
		}
	}
	for(i=1;i<=n;i++) printf("%d ",dis[i]);
}
int main()
{
	scanf("%d%d%d",&n,&m,&s);
	fill(head,head+n+1,-1);
	while(m--)
	{
		int u,v,w;
		scanf("%d%d%d",&u,&v,&w);
		add(u,v,w);
	}
	dijkstra();
	return 0;
}